DFT in solids

DFT in solids#

1.  Recap of DFT#

1. Kohn-sham equation (Auxiliary method)

\[ (-\frac{1}{2}\nabla + \underset{V_{eff}(\vec{r_1})}{\underbrace{{V_{ne} +V_H+V_{xc}}}})\, \theta_i (\vec{r_1}) = \epsilon_i \theta_i(\vec{r_i}) \]
2. SCF Loop

3. \(\mathbf{E_{xc}[\rho]}\)

  • LDA: uniform electron gas \(E_{xc}^{LDA}-\int\rho(\vec{r})\epsilon_{xc}[\rho(\vec{r})]d\vec{r}\)

\(\epsilon_{xc} = \underset{\text{exchange}}{\underbrace{\epsilon_x}} + \underset{\text{correlation}}{\underbrace{\epsilon_c}}\)

e.g. VWN, PZ, PWQ, SPZ

Effective but over-binding

  • GGA: add \(\nabla \rho(\vec{r})\) (Non-homogeneity)

\(E_\text{xc}^\text{GGA} = \int f(\rho,\nabla \rho)d\vec{r}= E_\text{x}^\text{GGA}(\rho) +E_\text{c}^\text{GGA}(\rho)\)

e.g. PBE, BLYP, …

Very good property results, mostly used for geometries, energies.

  • self interaction problem

In HF, \(E_x^{HF}+E_H = 0\) , when \(i=j\) (Cancelled)

In DFT, not fully cancelled out.

  • Hybrid functional:

Mix DFT with HF

e.g. B3LYP: adjustable parameters

​ PBEO: \(25\% E_x^{HF} + 75\% E_x^{PBE} + E_c^{PBE}\)

​ HSE06: adjustable parameters, solid

  • 4. Jacob ladder:

\(\text{LDA}\rightarrow \text{GGA}\rightarrow \text{meta-GGA} \rightarrow \text{hybrid functional}\rightarrow \text{exact solution}\)

2.  Periodic structures#

[!NOTE]

The Bravais Lattice: The positions and types of atoms in the primitive cell form the basis. The set of translations, which generate the entire periodic crystal by repeating the basis, is a lattice of points in space called the Bravais Lattice.

\[ \text{Crystal structure} = \text{Bravais Lattice} + \text{basis} \]

Primitive Cell:

  • Smallest unit cell

  • Fill whole space through translation

  • It has a single lattice point

Wigner-Seitz unit cell (unique primitive cell):

Translation:

\[ T(\vec{n}) = n_1\vec{a_1}+ n_2\vec{a_2}+...+n_d\vec{a_d} =\sum_i^d n_i\vec{a_i} \]
For FCC:

Primitive lattice vector: \(\vec{a_1} &= (0,\frac{1}{2},\frac{1}{2})\\ \vec{a_2}&=(\frac{1}{2},0,\frac{1}{2})\\\vec{a_3}&=(\frac{1}{2},\frac{1}{2},0)\) Conventional lattice vector: \(\vec{a_1} &= (1,0,0)\\ \vec{a_2}&=(0,1,0)\\\vec{a_3}&=(0,0,1)\)

Volume:

\(d=1,& |\vec{a_1}|\\d=2,& |\vec{a_1}\times \vec{a_2}|\\d=3,& |\vec{a_1}\times \vec{a_2}\times \vec{a_3}|\) or \(V = \det|a_{ij}|\)

Space group:

Translation group + point group

Symmetry group: group of symmetry transformations, e.g. rotation, reflection, inversion

3.  The Reciprocal Lattice and Brillouin Zone#

4.  The Bloch Theorem#

Introduces the periodicity of the crystalline potential (of the unit cell) into the wave function:

\[ \Psi_i(\vec{r},\vec{k}) = e^{i\vec{k}\cdot\vec{r}}\,\mu_{\vec{k}}(\vec{r}) \]

  • \(k\) is the wave vector, \(\vec{k} = k_1\vec{b_1}+k_2\vec{b_2}+k_3\vec{b_3}\)

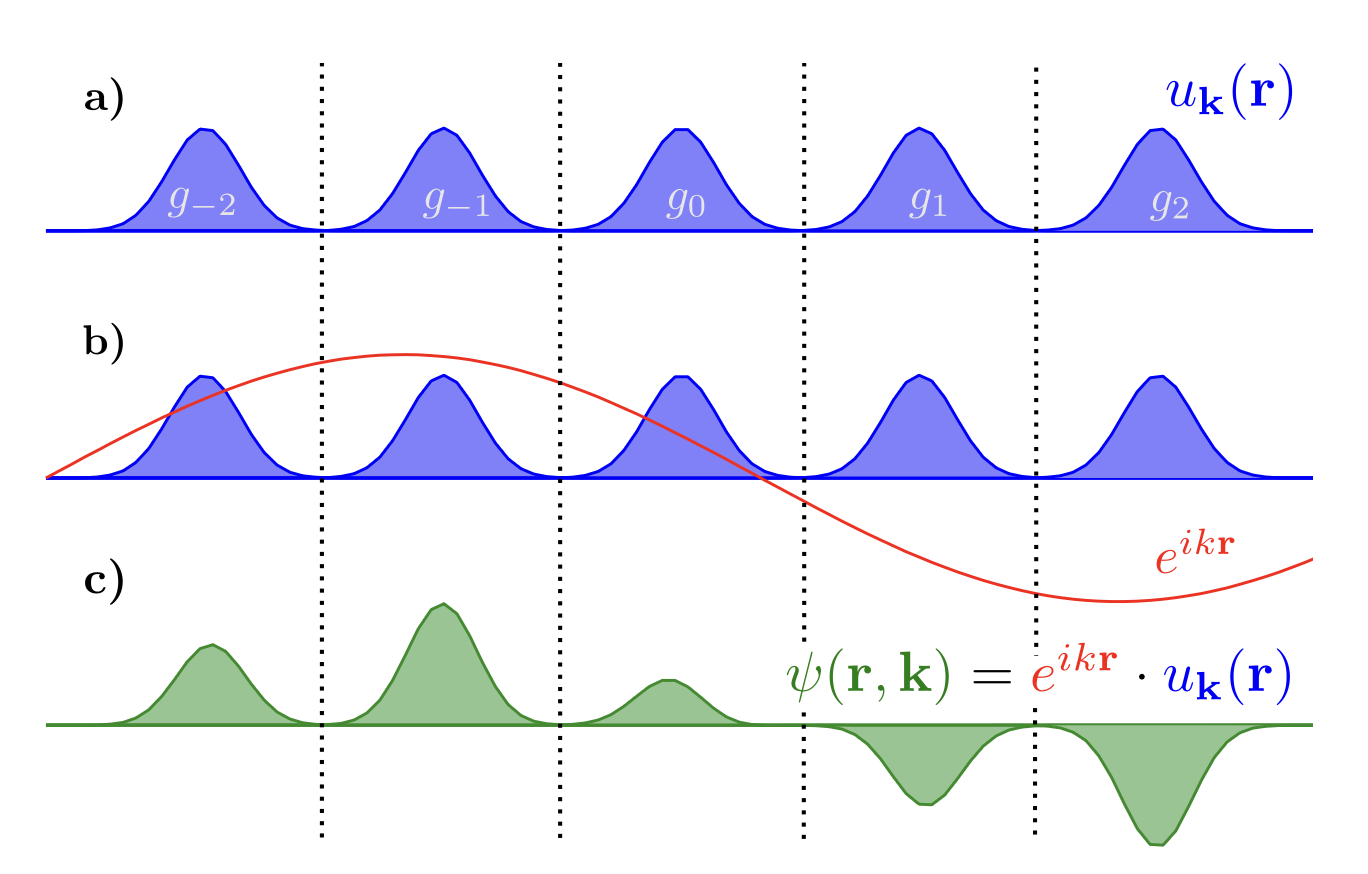
image-20251028164029605

5.  Plane-wave basis set#

For charge density:

\[\begin{split} \rho_n(r) = \int\Psi_{nk}(r)^\star\Psi_{nk}(r)dr\\ \overset{\text{Bloch theorem}}{\Rightarrow} = \int \left(e^{-i\mathbf{k}\cdot\mathbf{r}} u_{n\mathbf{k}}^\star(\mathbf{r})\right) \left(e^{i\mathbf{k}\cdot\mathbf{r}} u_{n\mathbf{k}}(\mathbf{r})\right) d\mathbf{k} \\ = \int |u_{n\mathbf{k}}(\mathbf{r})|^2\, d\mathbf{k} \end{split}\]
So, how to represent \(\Psi_{nk}(r)\), \(\Rightarrow\) plane wave basis set + pseudo-potential

Plane-wave:

\[\begin{split} \text{Expand:} \, \Psi_{nk}(r)=\frac{1}{\sqrt{\Omega_\text{cell}}}\sum_{\vec{G}}e^{i(k+G)r}\cdot C_{Gnk}\\ \sum_{\vec{G}}|C_{Gnk}|^2=1 \end{split}\]

[!NOTE]

PW vs LCAO:

PW:

  1. +: Orthonormal

  2. +: Independent of atomic positions

  3. +: No basis set superposition errors (BSSE)

  4. -: Large basis set (expensive to compute)

  5. -: Hard to deal with localized orbitals

LCAO:

  1. +: Chemistry insight

  2. +: Small basis set (cheaper to compute)

  3. -: not orthogonal

  4. -: depends on atomic positions

  5. -: BSSE

Plane-waves Cut-Off

Due to the PW expansion remains exact in the limit of an infinite number of G-vectors and all the plane waves fulfill the condition of orthonormality. However, in real situations, we can only have limit plane waves. To determine that:

\[ \frac{1}{2}|\mathbf{k} + \mathbf{G}|^2 \le E_\text{cutoff} \]

6.  DFT for Solids in the Plane-Wave Formalism#

\[ E_{\mathrm{KS}}[\rho] = T_s[\rho] + \int d\mathbf{r}\, V_{\mathrm{ne}}(\mathbf{r})\rho(\mathbf{r}) + E_{\mathrm{Hartree}}[\rho] + E_{nn} + E_{\mathrm{xc}}[\rho] \]

In solids:

\[ (-\frac{1}{2}\nabla_i^2 + V_\text{eff}(\vec{r_i}))\Psi_{n\vec{k}}(\vec{r}) = \epsilon_{n\vec{k}}\Psi_{n\vec{k}}(\vec{r}) \]
Solve KS equation for solids:

  1. Choose \(E_\text{cutoff}\quad \&\quad\text{k-points grid}\)

  2. Compute \(\rho(r)=\frac{1}{\Omega_{Bz}}\sum_n \int_{BZ}f_{nk}|\Psi_{nk}(r)|^2dk\)

7.  Pseudopotential#

To deal with the external potential term \(V_\text{ne}\) : Plane wave is expensive since we need large basis set, the reason is \(V_\text{ne}(\vec{r_\text{ne}}) =-\frac{\mathcal{Z}_A}{|\vec{r_A}-\vec{r_i}|}\), when \(\vec{r_{ne}}\rightarrow 0\Rightarrow \text{singularity of } V_{ne}\), so, \(V_{ne}\) is very oscillate near core! It’s very hard to fit and needs more PW.

Examples:

  • Non-conserving PP (NCPP): integrated charge \(r<r_c\), same as all electron case

  • Ultrasoft PP (USPP): Relax norm-conservation then add augmentation charge to recover the correct charge density \(\rho\)

  • Projector augmented wave PP (PAW-PP): Reconstruct all electron wave function from pseudopotential using projectors.

Contents