MolGAN: An implicit generative model for small molecular graphs

MolGAN: An implicit generative model for small molecular graphs#

1.  Introduction#

image-20240625171220358

Sidestep this issue by utilizing implicit, likelihood-free methods, in particular, a generative adversar- ial network (GAN) that we adapt to work directly on graph representations. We further utilize a reinforcement learning (RL) objective similar to ORGAN (Guimaraes et al., 2017) to encourage the generation of molecules with particular properties.

2.  Background#

2.1.  Molecular graph#

Undirected graph G with a set of edges \(\xi\) and nodes \(V\) .

  • Each atoms correspond to a node \(v_i \in V\) that is associated with a T-dimensional one-hot vector \(x_i\)

  • Represent Atomic bond as an edge \((v_i,v_j)\in \xi\) associate with a bond type \(y\in \) {\(1,...,Y\)}

For molecular graph with N nodes

Node feature matrix \(X=[X_1,...,X_N]^T\in R^{N\times T}\)

Adjacency tensor \(A\in R^{N\times N\times Y}\) where \(A_{ij}\in R^Y\) is a one-hot vector indicating the type of edge between \(i\) and \(j\).

2.2.  Generative adversarial networks#

  1. Generative model \(G_\theta\), learns a map from a prior to the data distribution to sample new data-points.

  2. Discriminative model \(D_\phi\), learns to classify whether samples came from the distribution rather than from \(G_\theta\).

Those two models are implemented as neural networks and trained simultaneously with stochastic gradient descent (SGD).

\[ \min_{\theta} \max_{\phi} \mathbb{E}_{x \sim p_{data}(x)} [\log D_{\phi}(x)] + \mathbb{E}_{z \sim p_z(z)} [\log (1 - D_{\phi}(G_{\theta}(z)))] \]
where \(G_\theta\) tries to generate samples to fool the discriminator and \(D_\phi\) tries to differentiate samples correctly.

3.  Model#

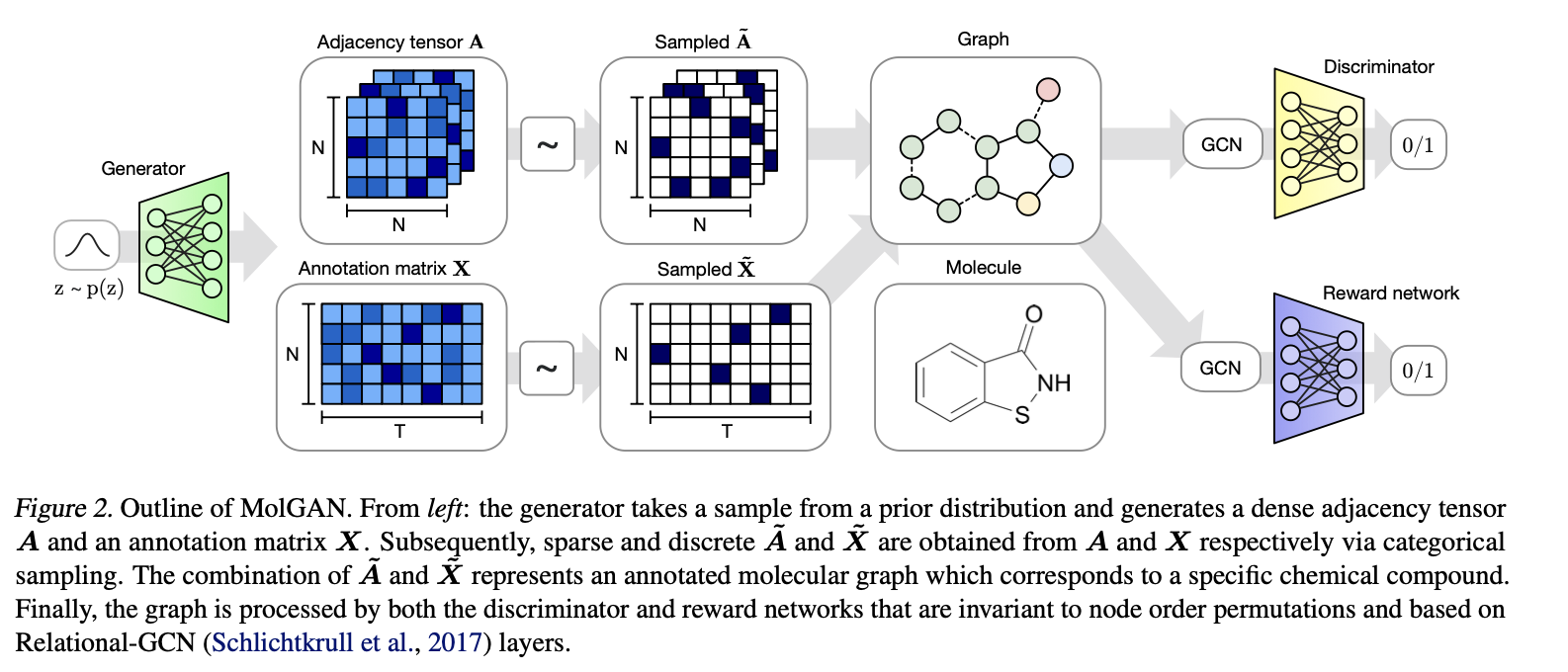
image-20240625212658747

Components: a generator \(G_\theta\) , a discriminator \(D_\phi\) , and a reward network \(\hat{R}_\psi\)

The reward network is used to approximate the reward function of a sample and optimize molecule generation to- wards non-differentiable metrics using reinforcement learning.

3.1.  Input of the model#

  • Generator: \(z \sim p_z(z)\) , A noise vector z sampled from a prior distribution \(p_z(z)\) .

  • Discriminator: \(x\sim P_{data}(x)\) and \(G_\theta(z)\)

  • Reward network: Dataset and generated samples are inputs of \(R^\psi\) ,different from discriminator, it assign scores to the molecular graph (e.g., to be easily synthesizable) by RDkit.

3.2.  Generator#

​ \(z\in R^D\) and \(z \sim \mathcal{N}(0, I) \)

​ \(z\longrightarrow G_\theta \longrightarrow\left\{\begin{aligned}&X\in R^{N\times T}\\&A^{N\times N\times Y}\end{aligned}\right.\)

Because both X and A have a probabilistic interpretation since each node and edge type is represented with probabilities of categorical distributions over types. To generate a molecule we obtain discrete, sparse objects \(\tilde{X}\) and \(\tilde{A}\) via categorical sampling from X and A, respectively. We overload notation and also represent samples from the dataset with binary \(\tilde{X}\) and \(\tilde{A}\).

As this discretization process is non-differentiable(Two strategies):

i.Use continuous \(X\) and \(A\) directly during the forward pass.

ii. Add Gumbel noise to \(X,A\) before passing to \(D_\phi\) and \(\hat{R}_\psi\).

​ i.e. \(\tilde{X_{ij}}=X_{ij}+Gum(\mu=0,\beta=1)\),

​ \(\tilde{A_{ijy}}=A_{ijy}+Gum(\mu=0,\beta=1)\)

iii. Use a straightthrough gradient based on categorical reparameterization with the Gum-softmax.1

​ i.e. \(\tilde{X_i}=Cat(X_i),\tilde{A_{ij}=Cat(A_{ij})}\)

3.3.  Discriminator and reward network#

Both the discriminator \(D_\phi\) and the reward network \(R^\psi\) receive a graph as input, and they output a scalar value each.

A series of graph convolution layers convolve node signals \(\tilde{X}\) using the graph adjacency tensor \(\tilde{A}\). At every layer, feature representations of nodes are convolved/propagated according to:

\[\begin{split} &h_i^{\prime (l+1)}=f_s^{(l)}(h_i^{(l)},x_i)+\sum_{j=1}^N \sum_{y=1}^Y \frac{\tilde{A}_{ijy}}{\mathcal{N}_i}f_y^{(l)}(h_j^{(l)},x_j),\\ &h_i^{(l+1)}=\tanh(h_i^{\prime (l+1)}) \end{split}\]
Where:

  • \(h_i^{(l)}\) is the signal of the node \(i\) at layer \(l\).

  • \(f_s^{(l)}\) is a linear transformation function that acts as a self connection between layers.

  • \(f_y^{(l)}\) an edge type-specific affine function for each layer.

  • \(\mathcal{N}_i\) denotes the set of neighbors for node \(i\).

After several layers of propagation via graph convolutions, we can aggregate node embeddings into a graph level representation vector as:

\[\begin{split} h^\prime_\mathcal{G}=\sum_{v\in\mathcal{V}}\sigma(i(h_v^{(L)},x_v))\odot \tanh(j(h_v^{(L)},x_v)),\\ h_{\mathcal{G}}=\tanh h^\prime_{\mathcal{G}} \end{split}\]
Where:

  • \(\sigma(x)=1/(1+exp(-x))\text{ is the logistic sigmoid function.}\)

  • \(i\text{ and }j\) are MLPs with a linear output layer.

  • \(\odot\) denotes element-wise multiplication.

  • \(h_{\mathcal{G}}\) is a vector representation of graph \(\mathcal{G}\) and it is further processed by an MLP to produce a graph level scalar output \(\in(-\infin,+\infin)\) for the discriminator and \(\in (0,1)\) for the reward network.

4.  Additional information#

Hadamard product(Element-wise multiplication)

For two matrices A and B of the same dimension \(m\times n\), the Hadamard product \(A\odot B\) is a matrix of the same dimension as the operands.

\((A\odot B)_{ij}=(A)_{ij}(B)_{ij}\)

Reference#

Contents