Lecture 8

Electron density \(\mathbf{\rho(r)}\)

For a multi-electron wave function \(\Psi(x_1, x_2, \ldots, x_N) \rightarrow \underset{\underset{x,y,z}{\text{Spatial}}}{3N} + \underset{\text{Spin}}{N}\) variables \(\rightarrow\) It is quire complex!

So, we use density to describe it:

\[ \rho(r)=N\int...\int|\Psi(x_1, x_2, \ldots, x_N)|^2dx_1dx_2,...,dx_N \]

Properties:

1. \(\rho(r\rightarrow\infty)=0\)

2. \(\int\rho(r)dr=\underset{\text{num of electrons}}{N}\)

Functional: function of functions

	Input	Output	Example
Function	Number	Number	\(f(x)=\sin(x)\)
Functional	function	Number	\(F[\rho(r)]\), \(\int_{-\pi}^{\pi}\sin(x)dx\)
Operator	function	function	\(H\Psi= \hat{H}\Psi\)

---

1.  The Hohenberg-Kohn Theorems

Theorem I: For any system of interacting particles in an external potential ( V_{\mathrm{ex}}(\mathbf{r}) ), the potential ( V_{\mathrm{ex}}(\mathbf{r}) ) is determined uniquely, except for a constant, by the ground-state particle density ( \rho_0(\mathbf{r}) ).

\[ E_\text{total}=\int\Psi^\star(r_1,...,r_N)\hat{H}\Psi(r_1,...,r_N)\rightarrow \underset{\text{Dirac notation}}{<\Psi|\hat{H}|\Psi>} \]

\[ \hat{H} = \underset{\text{kinetic}}{\underbrace{-\frac{1}{2}\sum_{i=1}^N \nabla_i^2}} + \underset{\text{nucleus--electron potential}}{\underbrace{\sum_{i=1}^N V(r_i)}} + \underset{\text{electron--electron interaction}}{\underbrace{\frac{1}{2}\sum_{i \ne j} \frac{1}{|r_i - r_j|}}} \]

\(E_{\text{total}}\) is a function of \(\Psi\), we indicate this property using square brackets:

\[ E_\text{Tot} = F [\Psi_i({r})] \]

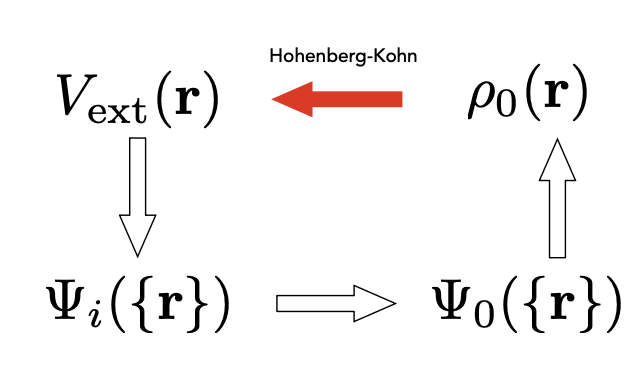
Theorem II: A universal functional for the total energy \(E[\rho]\) in terms of the density \(\rho(r)\) can be defined, valid for an external potential \(V_\text{ex}(r)\). For any particular \(V_\text{ex}(r)\), the exact ground state energy of the system is the global minimum value of this functional, and the density ρ® that minimizes the functional is the exact ground state density \(\rho_0(r)\).

---

2.  The Kohn-Sham Auxiliary System

Previous section describes how to represent multi-electron system into density form, using functional, but what functional looks like? How to solve it?

[!NOTE]

Same \(\rho_0(r)\), but not approximation compared with Hartree-Fock method.

The actual density functional theory calculations are performed on the auxiliary single-electron independent-particle system defined by the mono-electronic auxiliary hamiltonian \(\hat{H}_\text{aux}\), also known as the Kohn-Sham operator \(\hat{F}_\text{KS}\) in \(a.u.:^2\)

\[ \hat{H}_\text{aux}=\hat{F}_\text{KS}=-\frac{1}{2}\grad^2+V_\text{eff}(r) \]

[ \left{ \begin{aligned} &\text{eigenvalue}\rightarrow \theta_i® \quad\text{: K-S orbitals(one electron orbital)} \ &\text{eigenvalue}\rightarrow \epsilon_i \quad\text{:eigenvalue for orbital i} \end{aligned} \right. ]